Aufgabe A 1.1
Betrachten wir das Wachstum einer Palme.
Ihre Höhe beträgt zu Beobachtungsbeginn einen Meter, die momentane Wachstumsrate ihrer Höhe
wird durch die Funktion w mit
w(t)=4·(e-t)-e-2t); t≥0
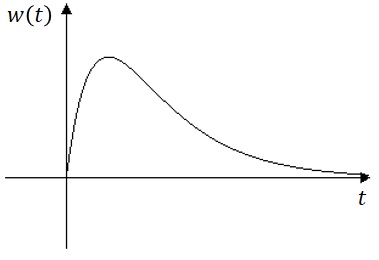
(t in Jahren nach Beobachtungsbeginn, w(t) in Meter pro Jahr) beschrieben.Die Abbildung zeigt den Graphen von w.
a) Geben Sie die momentane Wachstumsrate zum Zeitpunkt t=1 an.
Begründen Sie anhand des Graphen, dass die Höhe der Palme im abgebildeten Zeitraum nie abnimmt.
Die Funktion w besitzt im abgebildeten Bereich eine Wendestelle.
Beschreiben Sie die Bedeutung dieser Wendestelle im Sachzusammenhang.
Berechnen Sie den Zeitpunkt der maximalen momentanen Wachstumsrate.
(4 VP)
b) Berechnen Sie die Höhenzunahme der Palme im zweiten Jahr nach Beobachtungsbeginn.Bestimmen Sie einen integralfreien Funktionsterm der Funktion h, der die Höhe der Palme zum Zeitpunkt t angibt.
Ermitteln Sie rechnerisch den Zeitpunkt, an dem die Palme eine Höhe von 1,50 m hat.
Untersuchen Sie, welche Höhe die Palme maximal erreichen kann.
Formulieren Sie eine Fragestellung im Sachzusammenhang, die auf die Gleichung
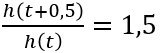führt.
(8 VP)
Aufgabe A 1.2
Für jedes a>0 ist eine Funktion fa gegeben durch
.
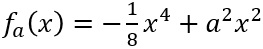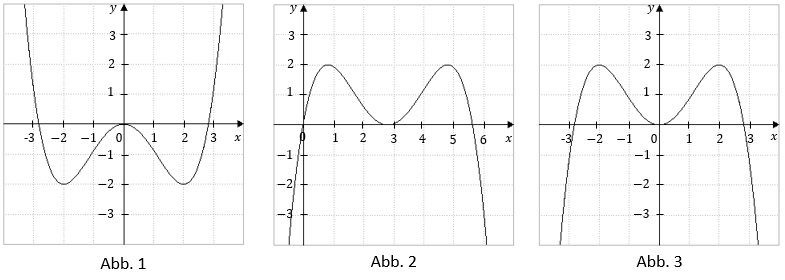
a) Abgebildet sind drei Graphen.
Begründen Sie, dass zwei dieser Graphen nicht zu einer Funktion fa gehören.
Der verbleibende Graph gehört zu einer Funktion fa.
Bestimmen Sie den zugehörigen Wert von a.
(3 VP)
b) Jede Funktion fa besitzt an der Stelle x1=2a ein Maximum.Ermitteln Sie eine Gleichung der Kurve, auf der die zugehörigen Hochpunkte aller Graphen von fa liegen.
(2 VP)
c) Der Punkt O(0|0) sowie die Punkte P(4a|-16a4) und Q(-4a|-16a4) des Graphen von fa bilden ein Dreieck.Berechnen Sie denjenigen Wert von a, für den dieses Dreieck gleichseitig ist.
(3 VP)
| Downloads |
PowerPoint